1/3時 ・角柱や円柱の表面積を求めることができる。 ・角柱や円柱の表面積の求め方を理解する。 本時の学習内容「角柱や円柱の表面積の求め方を考えよう」を知る。 教科書143ページの「考えてみよう」に取り組む。 立体の「表面積」、「底面積L字型などの立体の体積の求め方をL字型などの平面の面積の求め方をもとに考え、直方体や立体の 体積の公式を活用して求めることができる。 コンピュータを活用する利点 「立体のL字型・U字型の体積」を求める学習はこれらの立体を分割統合して求めなければならない。 この学習は空間的な⑤ まとめて,角柱の体積は,底面積×高さの式で求められる。 この考え方は第5学年で学習した直方体の体積の求め方が基盤となっており,これを基に, 未習である角柱の体積の求め方を考え,解決していくことができる。このことを,児童自身

円錐の表面積の求め方 裏技の公式を覚えたらめちゃくちゃ簡単 中学や高校の数学の計算問題
立体の面積の求め方
立体の面積の求め方-1立方体と直方体 立方体の体積=1辺×1辺×1辺 立方体の表面積=1辺×1辺×6 直方体の体積=たて×よこ×高さ 2角柱と円柱 角柱・円柱の体積=底面積×高さ 角柱・円柱の表面積=底面積×2側面積 3角すいと円すい 角すいと円すいの体積=底面積×高さ×本単元で扱う立体の体積の求め方は,学習指導要領には以下のように位置づけられている。 第6学年 b 量と測定 (3)図形の体積を計算によって求めることができるようにする。 ア 角柱および円柱の体積の求め方を考えること。




体積の求め方 計算公式一覧
三角錐や四角錐などの体積は、底面積 $S$、高さ $h$ として、次の式で求められます。 角錐 (かくすい) の体積 \begin{align*} V = \frac{1}{3}Sh \end{align*} 体積 = 底面積 × 高さ ÷ 3 中1 数学 表面積の求め方 表面積の求め方と!円錐の側面積と中心角の簡単な裏ワザをごしょーかい!ページ数少ないです笑 塾で教えてもらいました(((( 学年 中学1年生, 教科書 新編 新しい数学1 東京書籍, 単元 立体の体積と表面積, キーワード 中1,数学,表面積,求め方,まとめ,裏ワザ,簡47 7 立体の体積と表面積 133 次の図の直方体の体積と表面積を求めよ。 ⑴ ⑵ ⑶ 137 次の図の立体の体積と表面積を求めよ。 ⑴ ⑵ 135 次の図の円柱の体積と表面積を求めよ。 ⑴ ⑵ ⑶ 134 右 の図は ,円柱とその展開図である。 次の問いに答えよ。
底面積の求め方 図形ごとの底面積の求め方の一覧を下記に示します。 立方体 ⇒ 縦×横 直方体 ⇒ 縦×横 円柱 ⇒ 半径×半径×314 四角柱 ⇒ (上底下底)÷2×高さ 三角柱 ⇒ 底辺×高さ÷2 円錐 ⇒ 半径×半径×314 四角錐 ⇒ (上底下底)÷2×高さ様々な立体の求め方について、底面積に着目させて求め方を考えさせます。 第一次(2/5~4/5時間) 四角柱及び三角柱、円の立体の体積の求め方を考える。 三角柱と角柱の体積を比べ、そこから底面積の形に着目し、「底面積×立体の体積を求めるには,体積の微分が断面積になることを利用します. すなわち,左端 a から座標 x までの区間にある体積を x の関数として V(x) で表し, x における断面積を S(x) とおきます. 上で復習した面積の求め方と同様にして ⊿V(x)≒S(x)⊿x ≒S(x)
立体の表面積の求め方 立体の表面積 とは 立体の表面全体の面積のこと をいいます。 立体の表面積の公式も一応示しますが、考え方を理解することができていればわざわざ公式を覚える必要はありません。 なので、求めるまでの考え方を特に注意して読み進めてください。 それでは角柱、円錐それぞれの表面積の求め方を確認していきます。面積を求めている間も,音声を消した状態で,動画をループ再生させ,必要なときに確認できるようにする 既習の円の面積の公式,周の長さを公式を黒板に掲示する 4 半径 4 cm,高さが 5 cm の円柱の表面積を求める では,この解き方を参考に他の円柱の立体の体積の求め方 これで,円錐の体積が円柱の体積の 三分の一 になっていることが示されたのですが,以上の議論は,「任意の立体について,基準となる軸に対して軸と垂直な平面による切断面の面積が分かれば,その立体の体積を定積分により求めることができる。
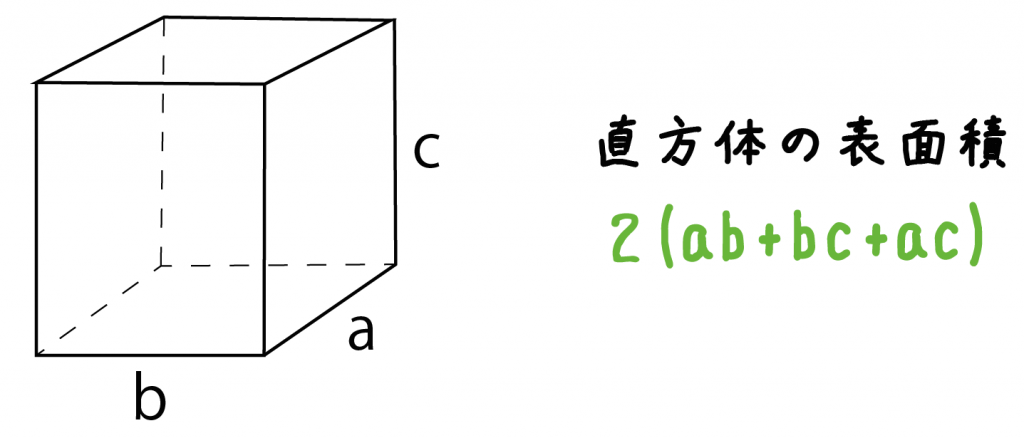



計算公式 直方体の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



立方体の表面積の求め方は 1分でわかる計算 公式 直方体の表面積の求め方
漢字のとおり、立体の 「表面の面積」 のことだよ。 底面や側面など、 すべての面の面積 を求めて、たし合わせよう。 立体の表面積を求めるときのポイントは、これだよ。立方体の12の辺の長さは等しく、これを $a$ とします。立方体の表面積 $S$ は、次の式で求められます。 立方体の表面積 \begin{align*} V = 6a^2 \end{align*} 表面積 = 一辺 × 一辺 × 6 うさぎでもわかる解析 Part27 2重積分の応用(体積・曲面積の求め方) こんにちは、ももやまです。 今回は2重積分を使って立体の体積や曲面積(表面積)を求める方法についてまとめています。 前回の記事(Part26)はこちら! 広義積分・ガウス積分に



Math 積み重ねた立方体の表面積 働きアリ




円錐の表面積の求め方 裏技の公式を覚えたらめちゃくちゃ簡単 中学や高校の数学の計算問題
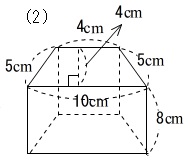
求める立体は①と②があわさって出来た立体であることから、①の直方体の体積+②の立方体の体積で求めることが出来ます。 ①の直方体の体積=8× 8×4 =256(cm³) ②の立方体の体積=4×4×4=64(cm³) よって求める立体の体積=256+64=3(cm³) さっそく、例題の表面積を求めてみよう。 底面が2つ、側面が1つだから、 9π×2 60π = 78π になるね! おめでとう!円柱の表面積の問題を瞬殺できるようになったね!! まとめ:「円柱の表面積の求め方」は公式なんかいらねえ!立体図形の体積と表面積の練習問題 問題1 次の立体の体積を求めなさい。 → 解答 問題2 次の立体の体積を求めなさい。 ただし、この立体は、どの面も(A)のようになっていて、それぞれの穴は反対の面までつきぬけているものとします。 → 解答




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




体積の求め方 計算公式一覧
たとえば、下の辺が4cm、上の辺が2 cm、高さ6cmの正四角錐台ABCDEFGHがあったとしよう。 この立体の体積は、 1/3 h ( a^2 ab b^2 ) = 1/3 × 6 × ( 4^2 4 × 2 2^2) = 2 × ( 16 8 4 ) = 56 cm^3 になるよ! めんどい計算式だけど、 落ち着いて計算してみよう! これで展開図の長方形のよこの長さがわかり、求めたい円柱の側面積がわかりますね。 底面の円周(長方形のよこの長さ)は 2×3×π=6π cm 円柱の側面積は 8×6π=48π cm 2 底面積は 3×3×π=9π cm 2数学・算数 立体の断面積の求め方 一辺の長さが2センチの立方体があります。(サイコロを机に置いた様子を考えてください)手前左上の頂点をaとし、反時計まわりに頂点をb,c,dとします。aの下の頂点を 質問no




体積 複雑な形の立体 算数 教科質問ひろば 進研ゼミ小学講座




計算公式 三角柱の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru「柱」の体積は、(底面積)×(高さ) 今回は 「立体の体積」 を求めるよ。 体積の求め方は、「すい」と「柱」に関して2つの公式を覚えてしまおう。立体(L字型) 解説 6年 分数のかけ算とわり算 円の面積の求め方 解説 円柱の体積 円柱の体積の求め方 解説 熊本市教育センター
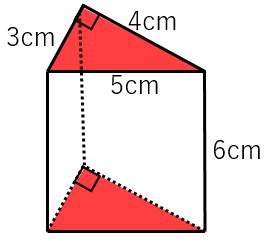



三角柱の底面積 側面積 表面積の求め方 具体例で学ぶ数学
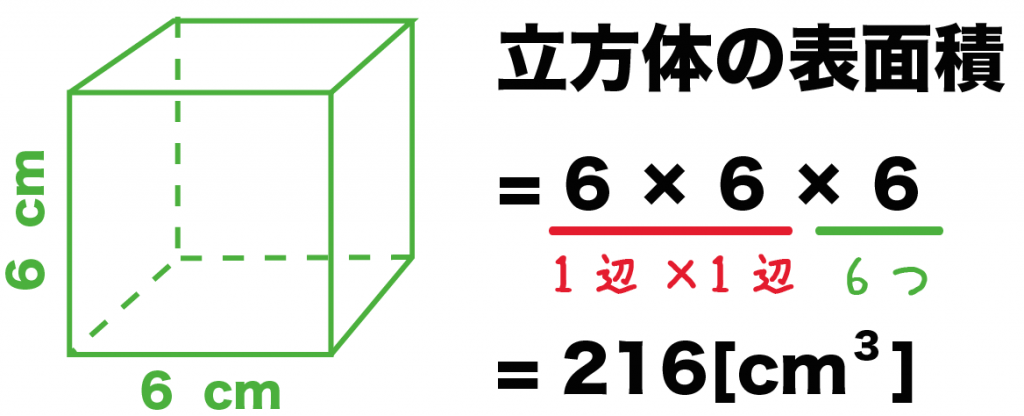



計算公式 立方体の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく
小問(2): bmnの求め方① obf(1㎝ 2)- bmn=四角形ofmnです。 「 bmnが obfの何分の1なのか」 が分かれば、 bmnの面積は求めることができます。 図c 今回は、相似な三角形である mbcと mraに注目します。(図c) bm:mr:rf=2:1:3となるため、 bmはbfの3分の1 だということが分かりました。 ※もし分から4年生の面積で、複合図形の面積の求め方 を 赤い線のように、横で二つの立体に分けます。 上の直方体の体積 10×4×(155)=400 下の直方体の体積 10×8×5=400 二つの立体の体積をあわせると =800 答え800 とき方 その3 下の図のように、縦10cm横8cm高さ15cmの大きな直方体の体積から、縦10cm横4cm立方体・直方体の体積の求め方|小学生に教えるための分かりやすい解説 管理人 9月 , 18 / 12月 1, 18 立体の体積という新しい分野なだけに、なかなかイメージしづらかったり、理解しづらい子は
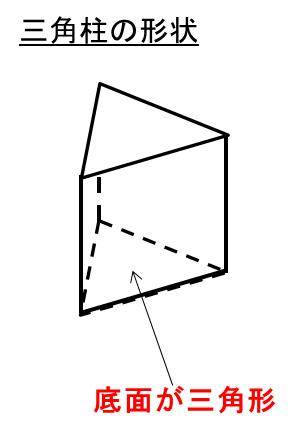



三角柱の表面積 底面積も と体積を求める公式と計算問題 単位との関係 ウルトラフリーダム




円柱の表面積と体積を求める公式 具体例で学ぶ数学
小学生の算数・図形・面積・体積に関する算数の問題プリント、練習プリントです。 無料でダウンロード、印刷してご利用いただけます。 小学1年生の算数 図形 練習問題プリント 小学2年生の算数 図形 練習問題プリント 小学3年生の算数 図形 練習問題指導にあたっては,「角柱の体積」では,直方体の求積公式の見直し, 公式の(縦)×(横)は底面に並ぶ 単位立方体の数と底面積を表す個数と等しいことに気づかせるために,底面における1㎤の立体模型の数と紙 の面積の数が等しいことを理解させ,直方体の体積が底面積×高さで考えられるようにする。この求め方を四 角柱や三角柱,さらに円柱にも適応できることに気付かせることから,底面 円柱の体積、表面積の求め方はこれでバッチリ! 円錐の表面積、中心角の求め方を解説!裏ワザ公式も!←今回の記事 円錐を転がすと1周するのにどれくらい回転する? 球の体積・表面積の公式はこれでバッチリ!語呂合わせで覚えちゃおう!




三角柱 四角柱 円柱の体積の求め方 具体例で学ぶ数学




中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン
半径がrの球の中心とその球面上面積がr 2 であるような円形の球面とを結んでできる円錐状の、立体の頂点部分の開き具合。球面全体は4πsrになります。 これは平面角のラジアンと同じ考え方ですが、立体ですので半径rの球体を考えます。円柱 複合図形の体積の求め方 図形を分けたり、合わせたりして自分の知っている形にする。 5㎝ 4㎝ 9㎝ 5㎝ 4㎝ 3㎝ 9 ㎝ 四角柱の底面の形に注目してみると cm 、下底9 、高さ3 平面の台形を高さ4 cm まで積み上げたと立体の名前 三角柱 円錐 六角柱 三角錐 円柱 底面の形 三角形 円 六角形 三角形 円 面の数 5 2 8 4 3 辺の数 9 なし 18 6 なし 頂点の数 6 1 12 4 なし 2長さの求め方について、下の( )に当てはまる言葉を入れなさい。 (1) 正方形の周 = 一辺の長さ×4 (2) 長方形の周 = (縦+横)×2 3面積(表
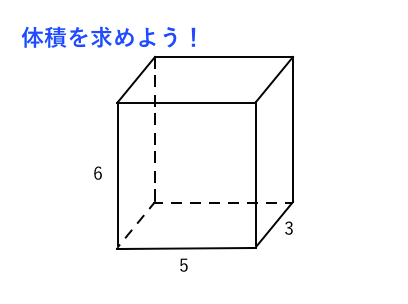



超簡単 体積の求め方 苦手な数学を簡単に




空間図形 角柱 角錐 すい 円柱 円錐の体積の求め方 中学数学 定期テスト対策サイト
底面の面積の求め方 青い部分は 横 8-5=3 たて 10-6=4 だから 底面積は 体積は 答え 580 下の三角柱の体積を求める問題では、どこが底面積でどこが高さかを考えさせることが大切です。 底面は必ずしも底にあるとは限りません。 上の場合は、横に2つある三角形の面が底面です。 下のA = 面積 P = 円周(近似式) 円錐 V = 体積 A = 円錐面積 r = d/2 = 半径 三角錐 V = 体積 S = 角錐底面積 角錐 角錐 pyramid V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径側面積= 側面の面積の総和 だから,円柱,角柱の表面積=底面積×2側面積 となります。 また,「底面積を求めよ」というときは,1つの底面の面積を答えます。



3




体積 表面積
公式一覧立体の体積・表面積の求め方(円柱・三角柱・円錐・三角錐・球) 体積の公式は何種類もあってわけわからなくなってしまう子が多いです。 ですが、仕組みを知ってしまえば無理して覚えずとも解くことができます。 まずはそれぞれ体積を求める



算数の問題です 1 図の立体は 円柱を半分に切った形です この立体の体積は何 Yahoo 知恵袋




三角柱の体積 表面積の求め方が図で誰でも即わかる 展開図も紹介 高校生向け受験応援メディア 受験のミカタ




計算公式 立方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




体積 容積の求め方 算数 教科質問ひろば 進研ゼミ小学講座




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット



3




中1数学 立体の表面積 例題編 映像授業のtry It トライイット




角柱 円柱の体積の公式 小学生に教えるための分かりやすい解説 数学fun




5年 直方体と立方体の体積 算数イメージ動画集 大日本図書
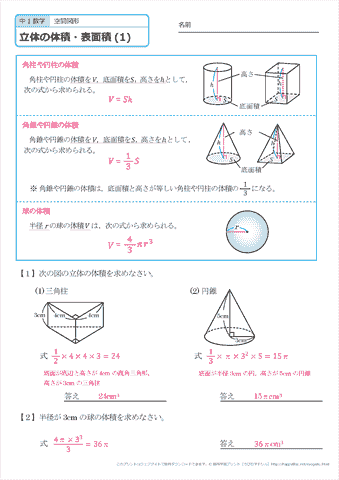



中学1年生 数学 空間図形 立体の体積と表面積 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
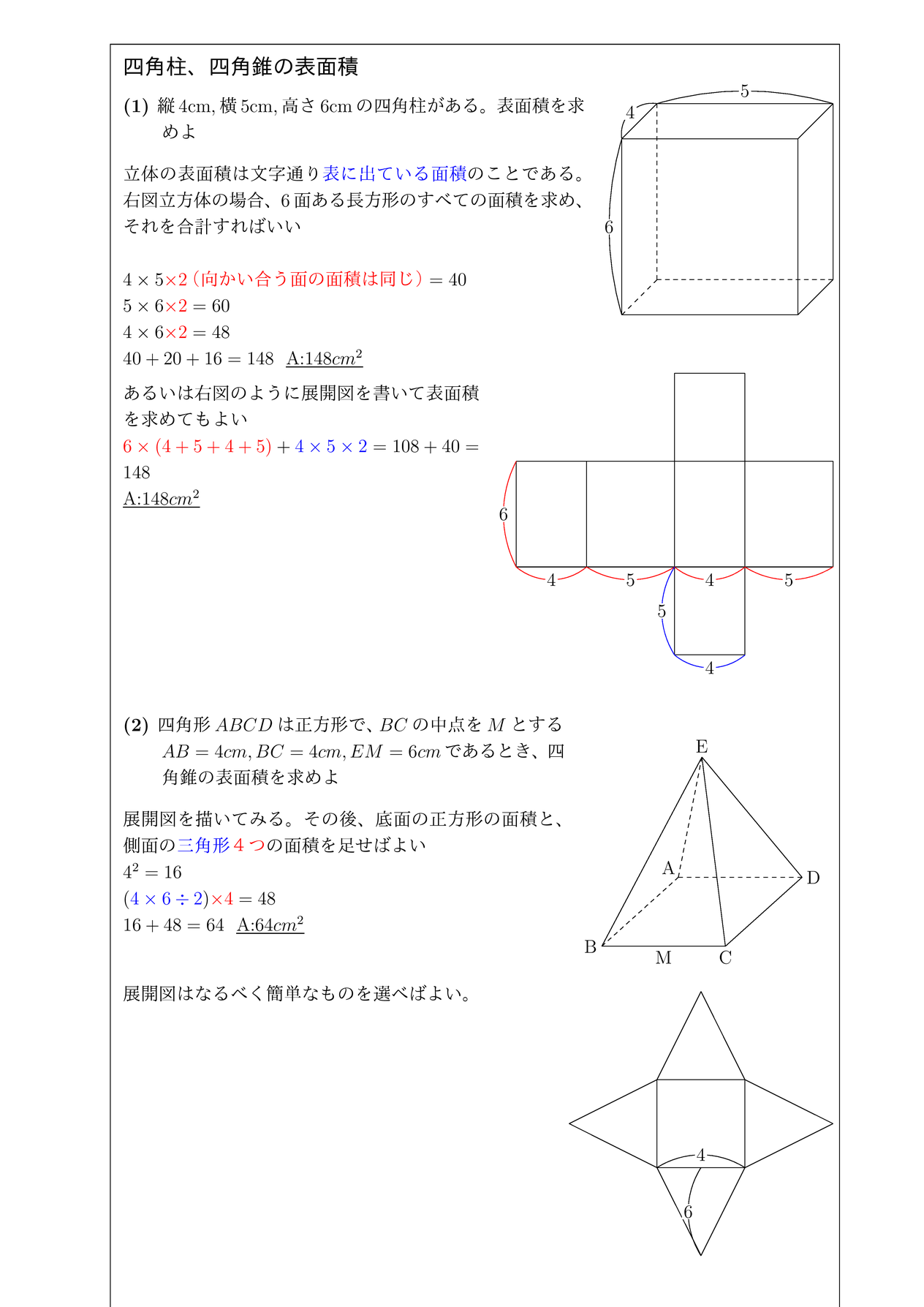



四角柱 四角錐の表面積 チーム エン




計算公式 立方体の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




体積の求め方 計算公式一覧



地図の体積計測
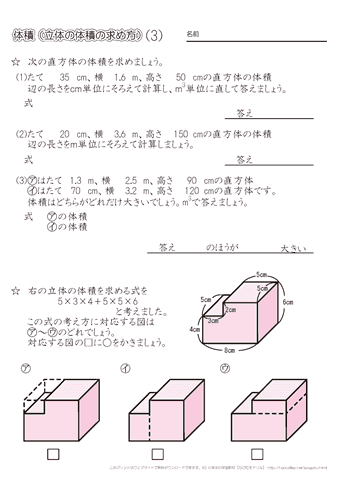



小学5年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生




立方体 直方体の体積の求め方 公式 小学生 中学生の勉強




立方体の表面積と体積を求める公式と計算問題 単位との関係も ウルトラフリーダム
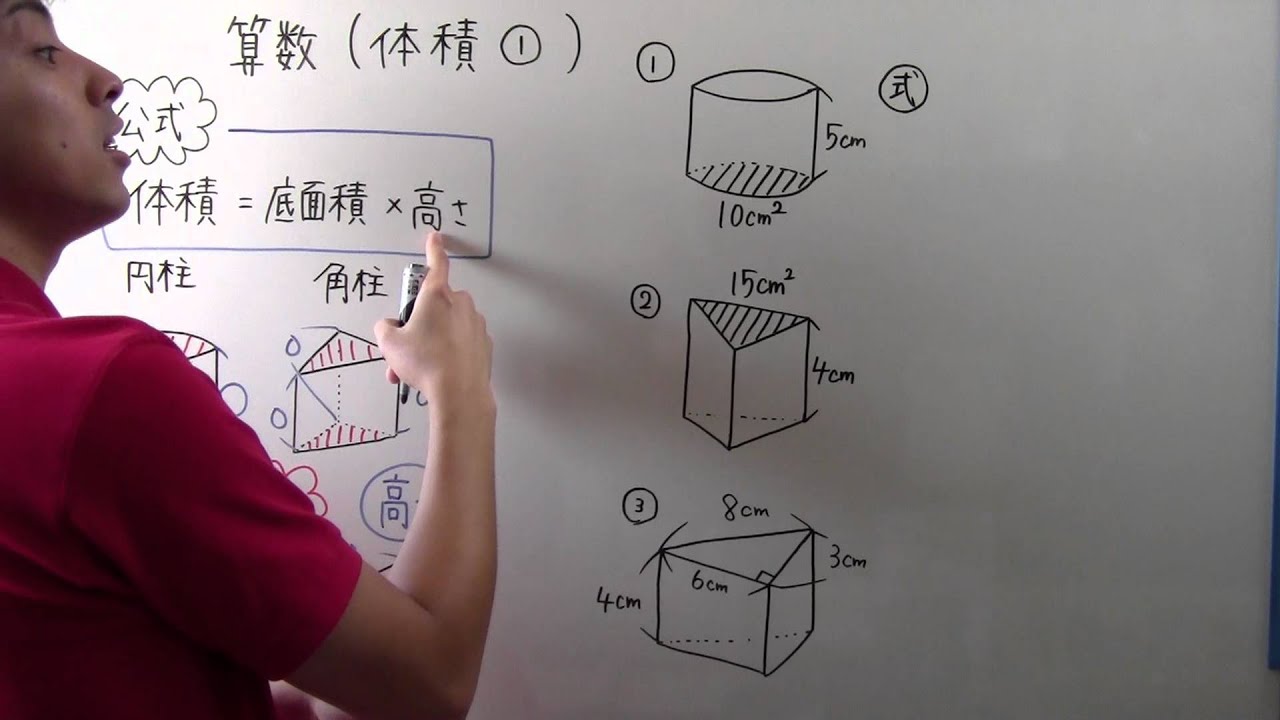



小6 算数 小6 25 体積 円柱 角柱 Youtube
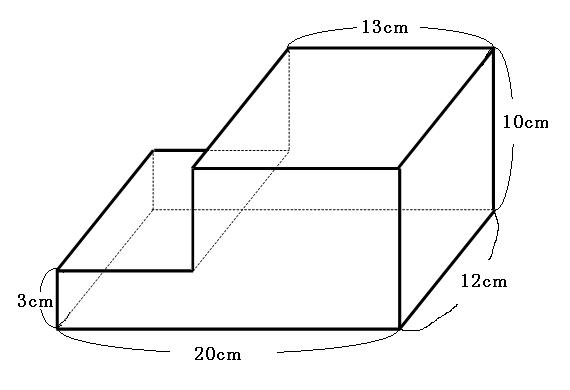



立体の表面積の求め方を解説 面倒な角柱や円柱の表面積をいかにサボって求めるか




三角柱の体積の求め方 小学生向けに問題使って解説するぞ 中学数学 理科の学習まとめサイト




小5 算数 小5 5 体積の求め方のくふう Youtube




空間図形 円柱の側面積の求め方がわかりません 中学数学 定期テスト対策サイト
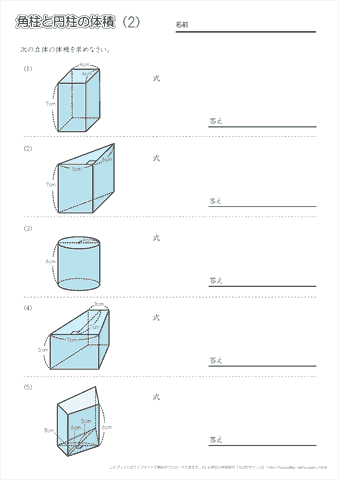



小学6年生の算数 角柱や円柱の体積の求め方 公式 問題プリント ちびむすドリル 小学生




円の面積の求め方を一通り身につけたら 少し応用的な問題にも挑戦してみましょう 円の面積の応用問題をやってみよう 円の面積の もっと基本的な問題のノート例はこちらです 円の面積 数学ノート 学習ノート 学習



6年算数立体の体積その2 教え方




立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




三角柱 四角柱 円柱の体積の求め方 具体例で学ぶ数学




円柱の表面積 Youtube



断面積とは 1分でわかる求め方 長方形と円の公式 単位 計算方法 直径との関係




立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者




立方体 直方体の体積の求め方 小学生に教えるための分かりやすい解説 数学fun
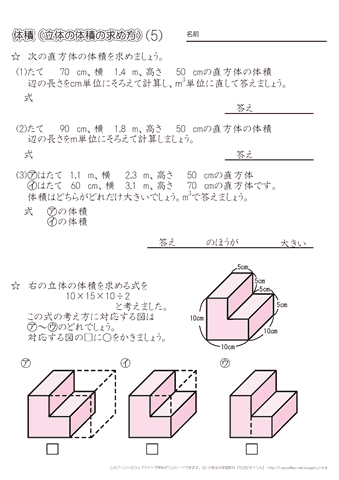



小学5年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生




円柱を2つ重ねた立体の表面積の求め方 Qikeru 学びを楽しくわかりやすく




公式を図解 すい体の体積 円すいの表面積の求め方




四角柱の表面積を求める問題なんですが 側面積 底面積をしても答えの通りになりませんで Clear




体積の求め方 立方体 長方体 小学生 算数のノート Clear
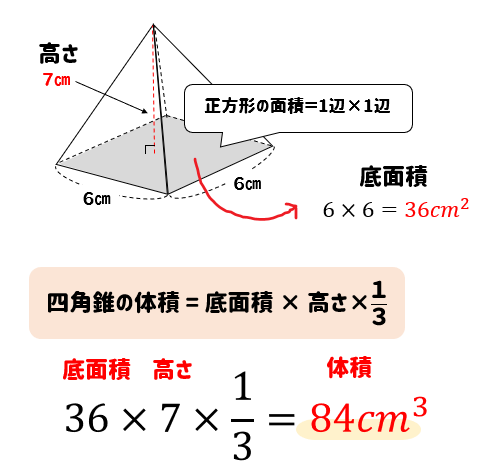



3分でなるほど 四角錐の体積 表面積の求め方をマスターしよう 数スタ




体積の求め方 計算公式一覧



底面積の求め方は 5分でわかる計算 円柱 円錐 四角柱 三角柱の底面積



5 5 複雑な立体の表面積と面積を求めるには さんすうがく
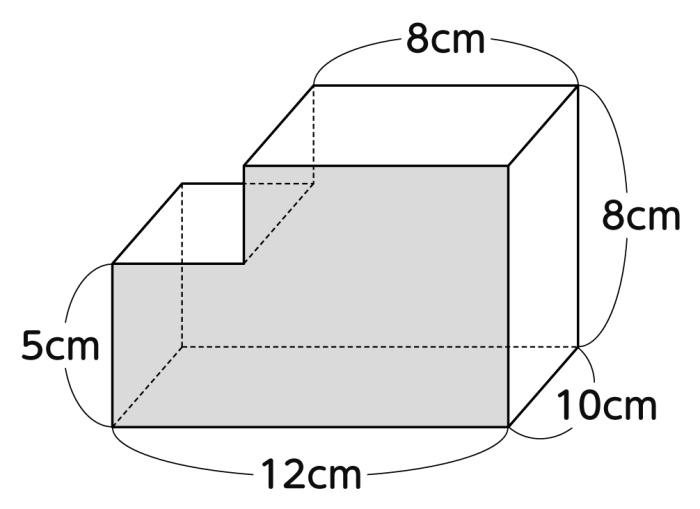



動画で学習 1 角柱と円柱の体積 算数




6年算数立体の体積1 教え方




3分でなるほど 四角柱の体積 表面積の求め方をマスターしよう 数スタ




立方体の表面積を求める計算と公式 辺と表面積の対応表つき Irohabook




スタディピア 立体の表面積




円柱の表面積と体積を求める公式 具体例で学ぶ数学




簡単 三角錐の体積 表面積の求め方と展開図が誰でもすぐわかる記事 高校生向け受験応援メディア 受験のミカタ



底面積とは 1分でわかる意味 求め方 円錐 三角錐 四角柱との関係 側面積との違い
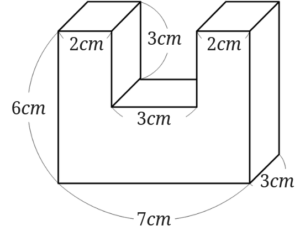



直方体や立方体の体積を求める応用問題の解き方は どうやって教えるといいの みけねこ小学校




公式を図解 すい体の体積 円すいの表面積の求め方



1




円柱の計算 体積 表面積の求め方はこれでバッチリ 数スタ




3分でなるほど 三角錐の体積 表面積の求め方をマスターしよう 数スタ




体積の求め方 公式一覧 小学生 中学生の勉強




立方体や直方体の体積の求め方を習ったら 少し応用的な問題にも取り組みましょう 展開図を見て 体積を求める問題や いくつかの立方体や直方体の面積を足したり引いたりして解く問題です 学習ノート 学習 数学ノート




3分で分かる 三角錐の体積 表面積の求め方 公式 練習問題 についてわかりやすく 合格サプリ




小学5年生の算数 体積 直方体と立方体を組み合わせた立体の体積を求める問題 ちびむすドリル 小学生



Studydoctor立体の体積の求め方と公式 柱体 中学1年数学 Studydoctor




三角柱の底面積 側面積 表面積の求め方 具体例で学ぶ数学




3分でなるほど 三角柱の体積 表面積の求め方をマスターしよう 数スタ




計算公式 円柱の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



直方体を組み合わせた立方体の面積 写真参照 を解きたいのですが Yahoo 知恵袋




角柱 円柱の表面積と体積の公式 数学fun



表面積や体積の求め方 三角柱 四角柱 円柱 球や半球



1



計算公式 立方体の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




計算公式 立方体の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




小5 複雑な立体の体積 直方体 日本語版 Youtube




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ



6 3 複雑な図形を1回転させてできる立体の体積と表面積を求めるには さんすうがく パート 2




体積の求め方 計算公式一覧




小5 算数 小5 3 直方体と立方体の体積 Youtube




角錐 円錐の体積と表面積の公式 数学fun



写真の底面が扇形の立体の表面積の求め方を教えてください 特に側面積が Yahoo 知恵袋




中1数学 立体の表面積と体積の求め方と練習問題 Pikuu




中1数学 三角柱 四角柱の体積の求め方がサクッとわかる 映像授業のtry It トライイット




中1数学 三角柱 四角柱の体積の求め方がサクッとわかる 映像授業のtry It トライイット



立体の表面積




中1 数学 中1 立体の表面積 Youtube




体積の求め方 計算公式一覧




計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




私の実践 私の工夫 算数 直方体や立方体の体積 児童が既習の知識と結び付けて考察できる授業を目指して 啓林館


